Sevgili okurlarım, bu konuda üniversitede eğitim almadım ama bol bol okuyorum ve konu çok çok ilginç. Ben de sizinle paylaşmak istedim. Yüzeyler ve boyutlar sözkonusu olduğunda hele hele uzayın şekil alması, insan kafası taş kesiliyor. Bir türlü kafamızda canlandıramıyoruz. Bakıyor bilimadamları işler karışıyor, “Efendim bu şekil böyledir ama yapılması bizim boyutta imkansızdır, işte en yakın benzeri 3 boyutla (yükseklik, genişlik ve en) bu kadar oluyor” diyorlar.”

Klein şişesi son derece cesur duruyor karşımızda ve gözlerimiz sabırla üzerinde geziyor. Hatlar müthiş kıvrımlı ve kadınsı(!) ama muamma son derece sert bir matematiğe dayalı. Önce şekle bir bakalım. Unutmayın aslında bu o şekil değil ona en yakın üretebildiğimiz bizim boyuttaki gölgesi diyelim. Yani “Anladım” demeyin, anlayan yok 🙂
“Şimdi ne oluyor yani bu ne şimdi?” diyenlere açıklayalım. Dikkatli bakınca iki tane giriş var ve iki tane son var. Ama tanımladıkları kapalı bir alan. Sonsuz bir kendi kendisine dönüş var ancak yine de çember gibi değil bir akış var. Bu şekli araştıran kişi Alman bilim adamı Felix Klein (1849-1925).
Ben de bir çok kişi gibi evrenimizin şeklinin bu türden bir uzaydan oluşup oluşmadığını merak ediyorum. Belki uzay gibi zamanın biçimsel enerjisel akışı da böyle bir yapı çiziyor zaman uzayıp kısalıp kendisiyle birleşiyor. Bilemiyorum. Belki bir karadelik modeli. Ancak herkes sıradışı bir oluşum ve model olduğuna emin. En kötüsü üst boyularda 4. 5. vs. farklı modelleri varmış bu şeklin tıpkı Mobious şeridi gibi!!!
Bu tür şekilleri ve yüzeyleri inceleyen bir bilim dalı var adı Topoloji (Dikkat Topoğrafya değil :)).
ALINTI
Topoloji
basitçe; şekillerin bükülerek, esnetilerek veya gerilerek deforme edildiğinde değişmeden kalan özellikleri inceler. bir şeklin kare mi daire mi, büyük mü küçük mü olduğunun topolojiyle ilgisi yoktur, çünkü uzatma işlemiyle bu özellikler değişebilir. topologlar bir şeklin bağlı olup olmadığını, delikleri olup olmadığını, boğumlu olup olmadığını sorarlar. yüzeyleri sadece eukleides’in bir, iki veya üç boyutlu evreninde değil, göz önüne getirilmesi imkânsız çok boyutlu uzaylar içinde hayal ederler. topoloji lastik yüzeyler üzerinde uygulanan geometridir. nicel olandan çok nitel olanla ilgilenir. (acid rain, 25.02.2005 19:07)
http://sozluk.sourtimes.org/show.asp?t=topoloji
İtiraf edeyim zorlandığımı hissettiğim az konudan biri 🙂 Lütfen siz de okuyun. Ben aktarırken yanlış aktarmaktan korktuğum için sözü Türkçe ve İngilizce kaynaklara bırakıyorum.
KAYNAKÇA:
Türkçe Kaynaklar
http://sci.ege.edu.tr/~mat/yazi/klein_bottle.html
http://www.formatd.net/metafor/galeri/2126klein.htm
http://sozluk.sourtimes.org/show.asp?t=klein+%C5%9Fi%C5%9Fesi&nr=y&pt=klein+sisesi
http://sozluk.sourtimes.org/show.asp?t=topoloji
http://sozluk.sourtimes.org/show.asp?t=manifold
http://www.matder.org.tr/bulten/mathart.asp?ID=27
http://sozluk.sourtimes.org/show.asp?t=mobius+seridi
http://sci.ege.edu.tr/~mat/yazi/mobius.html
İngilizce Kaynaklar
http://www.kleinbottle.com/
http://en.wikipedia.org/wiki/Klein_bottle
http://www.math.ohio-state.edu/~fiedorow/math655/Klein2.html
http://www.gakushuin.ac.jp/~881791/kuroki/Klein.GIF
http://mathworld.wolfram.com/KleinBottle.html
http://commons.wikimedia.org/wiki/Surfaces
http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Klein.html (Felix Klein)
X (Twitter) Takip Edebilirsiniz:
twitter.com/ssonmez
Bilimkurgu okumayı seviyorsanız,
Starbul ilginizi çekecektir. www.starbul.com
Youtube Kanalım:
www.youtube.com/suleymansonmez
Videolar
http://www.geom.uiuc.edu/~banchoff/Klein4D/KB-Rot3D.mpg
http://www.geom.uiuc.edu/~banchoff/Klein4D/KB-Rot4D.mpg
http://www.geom.uiuc.edu/~banchoff/Klein4D/KB-Sep.mpg
http://www.geom.uiuc.edu/~banchoff/Klein4D/Klein4D.html


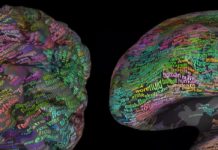








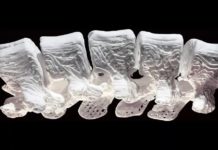

Süleyman abi şekiller çok güzel de, dışı sizi yakar içi bizi! Matematik bölümünde okuyup da topoloji dersiyle cebelleşince insanın “topoloji” kelimesini bir daha duyası gelmiyor 🙂
ya kaç gündür bakorum su sekle dört boyutta oluomus…nası bişi bu yaw:D
anadolu lisesinde öğrenciyim ve klein şişesiyle mobius şeridini araştırmayı istiyorum. topoloji hakkında çeşitli kitaplara ve internetteki kaynaklara baktım. ama çogunlukla cebirsel ifadelerle anlatılmış. yardım eder misiniz?
Ayça açıkçası bazen gelen yorumlar çok canımı sıkıyor. İnsan bir ödevi ararken bu kadar açık anlatıp üstte bir sürü siteye link vermişken neden gidip o sitelerden araştırıp ödevini yazmaz. Bizim yazar olarak sizin yerinize o sayfalara tıklamamız mümkün değil. Ayrıca telif hakları gereği o sayfalardaki yazıyı kendi sitemize çalıp yapıştırmayız da.
Size düşen görev bu denli hazır şekilde önünüze konulmuş bilgi de sadece tıklamak.
Madem yukarıdaki yazıyı okumak zor geliyor bir de buraya yapıştırayım
Türkçe Kaynaklar
http://sci.ege.edu.tr/~mat/yazi/klein_bottle.html
http://www.formatd.net/metafor/galeri/2126klein.htm
http://sozluk.sourtimes.org/show.asp?t=klein+%C5%9Fi%C5%9Fesi&nr=y&pt=klein+sisesi
http://sozluk.sourtimes.org/show.asp?t=topoloji
http://sozluk.sourtimes.org/show.asp?t=manifold
http://www.matder.org.tr/bulten/mathart.asp?ID=27
http://sozluk.sourtimes.org/show.asp?t=mobius+seridi
http://sci.ege.edu.tr/~mat/yazi/mobius.html
Gerçekten de çok ilginç , insanın kafası almıyor karışık ama mükemmel…